Machine Learning for Space Physics
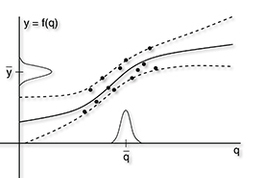
Deep Learning and Gaussian Processes
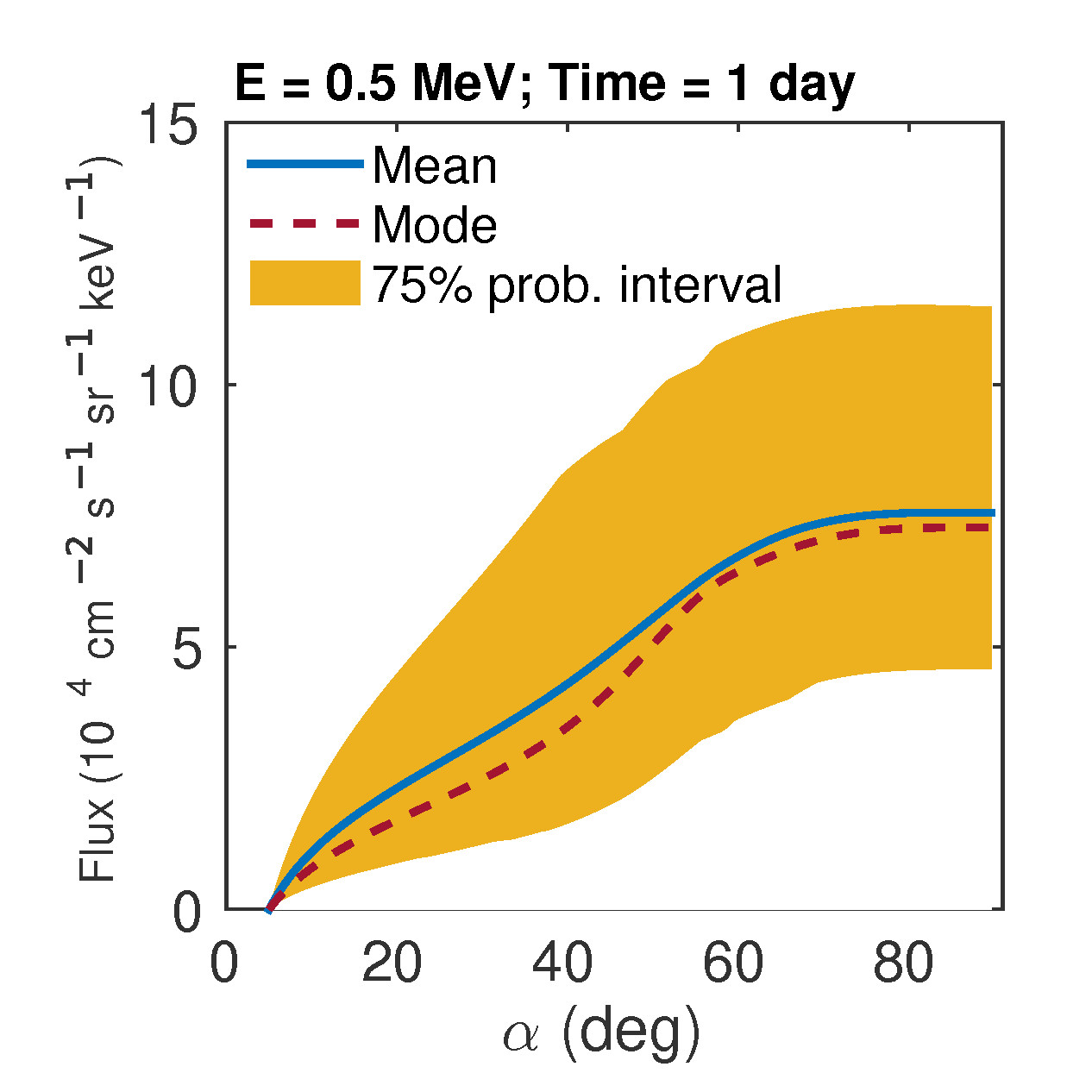
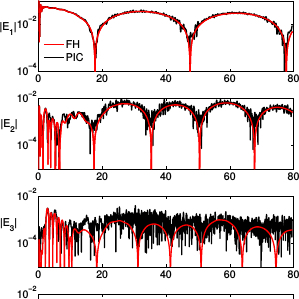
Can we use solar images and in-situ satellite data to train models that can predict Space Weather events? Can Machine Learning help in discovering new physics? The first book on the topic here.